集合论与图论

 

课程说明

教学内容 [Latest]

作业   [Latest] 

 

 

课程说明

一、课程性质和定位

离散数学是现代数学的重要分支，是一门重要的计算机专业基础课，是研究离散量的结构及相互关系的学科，它在计算机理论研究及软、硬件开发的各个领域都有着广泛的应用。

二、教学目的和任务

通过离散数学的教学，不仅能为学生的专业课学习及将来从事的软、硬件开发和应用研究打下坚实的基础，同时培养学生的抽象思维、严格的逻辑推理和创新能力。 离散数学是研究离散量的结构及其相互关系的数学科学。主要教学内容有集合论、代数结构、组合数学和数理逻辑。使学生掌握、处理离散结构的描述工具与方法，并能培养学生的抽象思维和严格的逻辑推理能力。

三、教学方式

本课程采用教师讲授、课堂讨论、学生实践相结合的教学方式，努力形成教师和学生双向互动的教学模式。

1 、教师课堂讲授是主要的课堂教学方式。

2 、在课堂教学过程中，注意充分发挥学生的自主性，鼓励学生积极提问和发言。

3 、在教师的指导下，学生有计划地、系统地进行自学。

四、课程考核与成绩评定

本课程为考试科目，采用考勤、平时成绩(作业、报告)、和期末考试成绩相结合方式，平时、期中成绩占40~50% ，期末考试成绩占50~60% 。成绩评定采用百分制，达到 60 分以上者为合格；

五、教材及参考书：

1 、《离散数学教程》，耿素云 屈婉玲 王捍贫编著，北京大学出版社

2 、《离散数学》，左孝凌，李为鉴，刘永才编著， 上海科技文献出版社

3 、《Elements of Set Theory》(集合论基础), Herbert B. Enderton, 人民邮电出版社

4、《Discrete Mathematics and Its Applications》(离散数学及其应用), Kenneth H.Rosen, 机械工业出版社

六、课时安排：

本课程周学时为 3 学时 。

教室：二教307

[校历] [万年历]

　

[TOP]

教学内容

课程介绍 [Intro]

第一章：集合 

   1.1. 预备知识：数理逻辑[slide]

    1.2.  集合的概念及集合之间的关系

    1.3.  集合的运算[slide] (背景介绍)

    1.4.  基本的集合恒等式[slide]

第二章：二元关系

  2.1.  有序对与卡氏积

  2.2.  二元关系  [slide]

  2.3.  关系矩阵和关系图

  2.4.  关系的性质

  2.5.  关系的幂运算[slide]

  2.6.  关系的闭包

  2.7.  等价关系和划分[slide]

  2.8.  序关系[slide]

第三章：函数[slide]

  3.1.  函数的基本概念

  3.2. 函数的性质

  3.3.  函数的合成

  3.4.  反函数

第四章：自然数[slide]

  4.1.  自然数的定义

  4.2.  传递集合

  4.3.  自然数的运算

第五章：基数[slide]

  5.1.  集合的等势

  5.2.  有穷集合与无穷集合

  5.3.  基数

  5.4.  基数的比较

  5.5.  基数运算

第七章：图

  7.1.  图的基本概念[slide]

  7.2.  通路与回路[slide]

  7.3.  无向图的连通性[slide]

  7.4.  无向图的连通度[slide]

  7.5.  有向图的连通性

第八章：欧拉图与哈密顿图[slide]

  8.1. 欧拉图

  8.2. 哈密顿图

第九章：树[slide]

  9.1. 无向树的定义及性质

  9.2. 生成树

  9.3. 环路空间

  9.4. 断集空间

  9.5. 根树

第十章：图的矩阵表示[slide]

  10.1. 关联矩阵

  10.2. 邻接矩阵与相邻矩阵

第十一章：平面图[slide]

第十二章：对偶图与着色[slide]

第十三章：

支配集、覆盖集、独立集与匹配[slide]

二部图中的匹配[slide]

复习 [slide] [集合论复习]

 

[TOP]

作  业

[#1]：（deadline: 2022.9.22）

 1. 用真值表证明以下等价式和蕴涵式

 

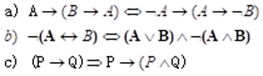
2. 不构造真值表证明1中各式

3. 把下面命题符号化，并求前束范式

   (1) “所有运动员都钦佩某些教练” ；

(2)“有些乌龟比有些兔子跑得快”；    

4. 给出一个解释，是下式左端为假，右端为真：

             "x(A(x) -> B(x)) => $xA(x)-> $xB(x)

P20：3，6，8，10

P21：13，16

P21：14，20，25(3),30(1)

 

 

[#2]：（deadline: ）

 

P53: 1

P54: 6, 7(1), 9, 11(2,4,5),12

P54: 16, 17, 19

P55: 21, 22, 27, 28

P55：29，31，35，37，39，45

P56：47，49，52

 

 

[#3]：（deadline:  ）

 

P68: 3，19，20

P80：2，3，5，7

P93：2，5，11，12

 

 

[#4]：（deadline: ）

 

P131: 1，2，3，5，7，11

P131：14，16，18，22，25

P143：4，7，13

P155：2，6，10, 11

 

 

[#5]：（deadline: ）

P164：2，4

P179：6，7，12，16

P189: 1，2，3，11，12，13

 

[TOP]    

　

　

　

致谢:

本课件参考屈婉玲老师, 刘田老师, 王捍贫老师的课件，

以及参考了很多网上可以下载的课件，无法一一列出出处。

在此感谢他们为本课程提供的资料与帮助！

　

[Home][Email]

© Peking University

Update: 2021.09.12